Question

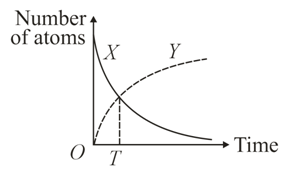
The graph represents the decay of a newlyprepared sample of radioactive nuclide X to a stable nuclide Y. The half-life of X is t. The growth curve for Y intersects the decay curve for X after time T. What is the time T?

• A. $ln\left(\right.t/2\left.\right)$
• B. $ln\left(\right.2t\left.\right)$
• C. $t/2$
• D. $t$

Answer 1

Answer: (D)

According to radioactive decay law, number of active nuclei of unstable nuclei at time $T$ is given by
$N_{1}=N_{0}e^{- \lambda T}....\left(1\right)$
and that for stable nuclei is given by
$N_{2}=N_{0}\left(1 - e^{- \lambda T}\right)....\left(2\right)$
where symbols have their usual meanings. We have assumed $\lambda $ as same for both nuclei.
$\therefore $ When graph intersects then
$N_{1}=N_{2}$
$\Rightarrow N_{0}e^{- \lambda T}=N_{0}\left(1 - e^{- \lambda T}\right)$
$\Rightarrow 2e^{- \lambda T}=1$
$\Rightarrow e^{\lambda T}=2$
$\Rightarrow \lambda T=ln2$
$\Rightarrow T=\frac{ln 2}{\lambda }=t_{1/2}=$ half life
Given, $t_{1/2}=t$
$\therefore T=t.$