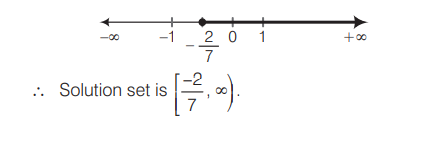Q. The graph of solution of the inequality $\frac{x}{2} \geq \frac{5 x-2}{3}-\frac{7 x-3}{5}$ on the number line is
Linear Inequalities
Solution:
We have, $\frac{x}{2} \geq \frac{(5 x-2)}{3}-\frac{(7 x-3)}{5}$
Taking LCM in RHS,
$ \frac{x}{2} \geq \frac{5(5 x-2)-3(7 x-3)}{15} $
$\Rightarrow \frac{x}{2} \geq \frac{25 x-10-21 x+9}{15} $
$\Rightarrow \frac{x}{2} \geq \frac{(25 x-21 x)-(10-9)}{15}$
$\Rightarrow \frac{x}{2} \geq \frac{4 x-1}{15} $
$\Rightarrow 15 x \geq 2(4 x-1) $
$\Rightarrow 15 x \geq 8 x-2$
Transferring the term $8 x$ to LHS,
$15 x-8 x \geq-2 \Rightarrow 7 x \geq-2$
Dividing both sides by 7 ,
$\frac{7 x}{7} \geq \frac{-2}{7} \Rightarrow x \geq-\frac{2}{7}$