Question

The graph of a polynomial $f ( x )$ of degree 3 is as shown in the figure and slope of tangent at $Q (0,5)$ is 3 .

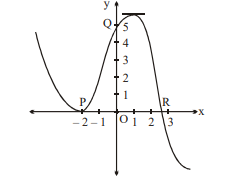
The equation of normal at the point where curve crosses $y$-axis, is

• A. $3 x+y=15$
• B. $x +3 y =15$
• C. $x+3 y=5$
• D. $3 x+y=5$

Answer 1

Answer: (B)

Let $f ( x )= ax ^3+ bx ^2+ cx + d$
$\therefore f (0)=5 \Rightarrow d =5$
So, $f(x)=a x^3+b x^2+c x+5$
$\therefore f ^{\prime}( x )=3 ax ^2+2 bx + c$
Now, $f ^{\prime}(-2)=0 \Rightarrow 12 a -4 b + c =0$....(1)
and $y=f(x)$ passes through $P(-2,0)$, so $0=-8 a+4 b-2 c+5$...(2)
Also, $f ^{\prime}(0)=3 \Rightarrow c =3$
$\therefore$ On solving, we get $a =\frac{-1}{2}, b =\frac{-3}{4}$
$\Rightarrow f(x)=\frac{-1}{2} x^3-\frac{3}{4} x^2+3 x+5$
Equation of normal at $Q(0,5)$ is
$(y-5)=\frac{-1}{3}(x-0) \Rightarrow x+3 y=15$