Q.
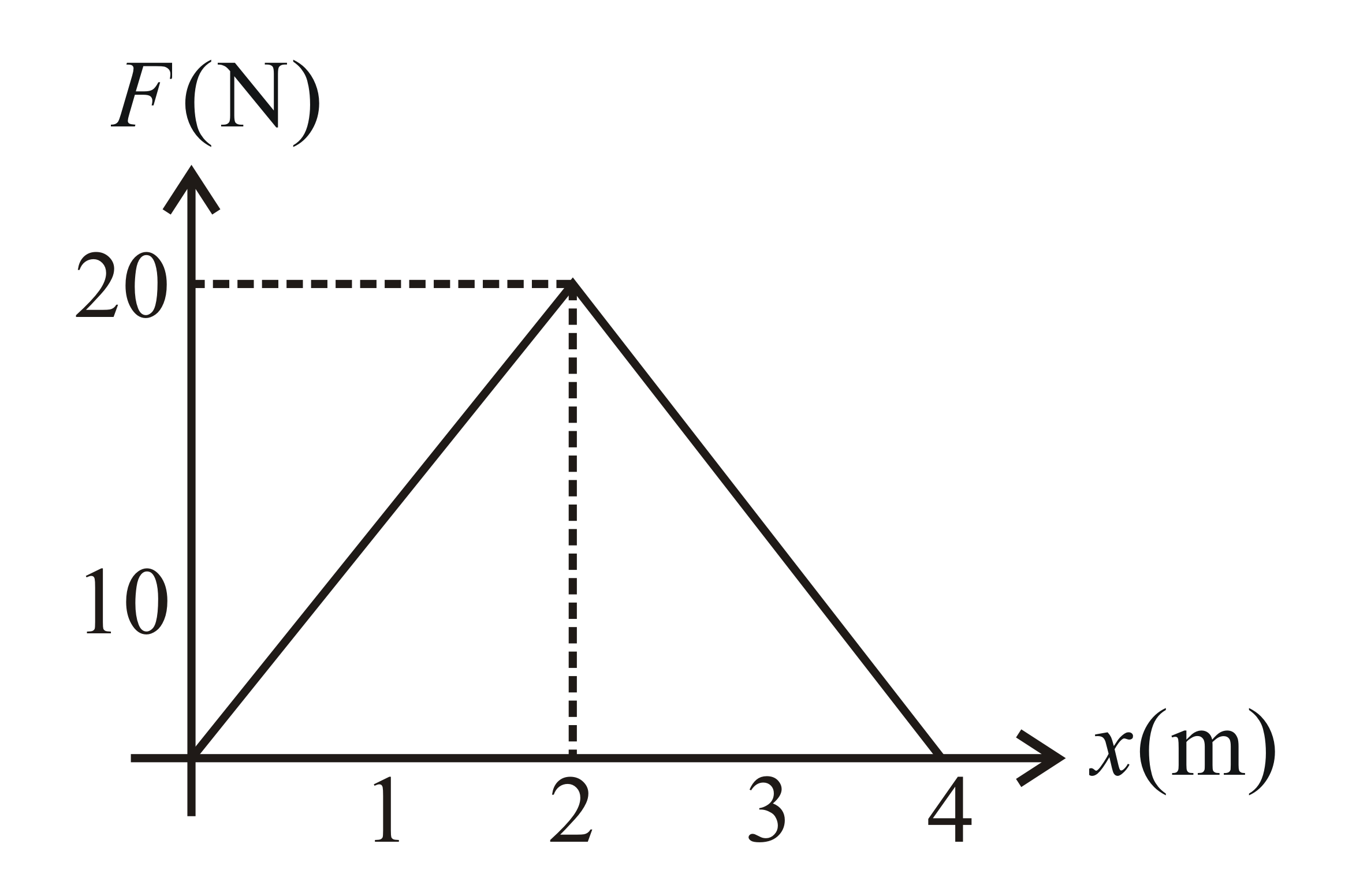
The graph between the resistive force $F$ acting on a body and the distance covered by the body is shown in the figure. The mass of the body is $25kg$ and initial velocity is $2ms^{- 1}$ . When the distance covered by the body is $4m$ , the value of its kinetic energy would be,
NTA AbhyasNTA Abhyas 2020
Solution:
Given:
$m=25kg$
$v_{initial}=2ms^{- 1}$
So, initial $KE$ of the body, $KE_{initial}=\frac{1}{2}mv^{2}=\frac{1}{2}\times 25\times 4=50 \, J \, $
Here, work done $=$ area of $F-x$ graph,
$\Rightarrow W=areaoftriangle\Rightarrow W=\frac{1}{2}\times base\times height\Rightarrow W=\frac{1}{2}\times 4\times 20\Rightarrow W=40J$
Since, the force is resistive. So, $W=-40J$ .
By work–energy theorem,
$Workdone=changeinkineticenergy$
$W=KE_{final}-KE_{initial}-40=KE_{final}-50KE_{final}=10J$
$m=25kg$
$v_{initial}=2ms^{- 1}$
So, initial $KE$ of the body, $KE_{initial}=\frac{1}{2}mv^{2}=\frac{1}{2}\times 25\times 4=50 \, J \, $
Here, work done $=$ area of $F-x$ graph,
$\Rightarrow W=areaoftriangle\Rightarrow W=\frac{1}{2}\times base\times height\Rightarrow W=\frac{1}{2}\times 4\times 20\Rightarrow W=40J$
Since, the force is resistive. So, $W=-40J$ .
$Workdone=changeinkineticenergy$
$W=KE_{final}-KE_{initial}-40=KE_{final}-50KE_{final}=10J$