Q.
The given lens is broken into four parts and rearranged closely as shown. If the initial focal length is $f$ then after rearrangement the equivalent focal length is
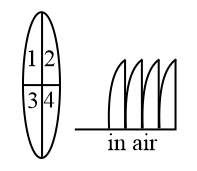
NTA AbhyasNTA Abhyas 2022
Solution:
