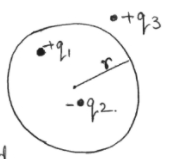
Question

The given figure shows a spherical Gaussian surface and a charge distribution. When calculating the flux of electric field through the Gaussian surface, the electric field will be due to

• A. $ +\,q_{3}$ alone
• B. $ +\,q_{1}$ and $ +\,q_{3}$
• C. $ +\,q_{1},+\,q_{3}$ and $ -\,q_{2}$
• D. $ +\,q_{1}$ and $ -\,q_{2}$

Answer 1

Answer: (D)

Shown a spherical Gaussian surface and a charge distribution.
The flux through the opherical Gaussian surface will be due to charges $+q_{1}$ and $-q_{2}$ only. Because, $q_{3}$ is outride surface.
So flux $=\phi =\frac{\text { net charge enclosed }}{\varepsilon_{0}}$
$\int E d s =\frac{\left(q_{1}-q_{2}\right)}{\varepsilon_{0}}$
$E\left[4 \pi r^{2}\right) =\frac{q_{1}-q_{2}}{\varepsilon_{0}}$
[$r= $ radius of sphere]
$E =\frac{\left(q_{1}-q_{2}\right)}{\varepsilon_{0}}\left[\frac{1}{r^{2}}\right]$
We can see that $E \alpha\left(q_{1}-q_{2}\right)$.
Thus, the electric field, while calculating flux through gaussian surface will be due to charges $+q_{1}$ and $-q_{2}$ only.