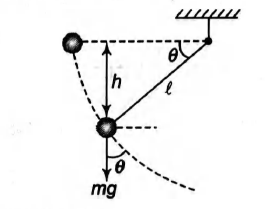
Question

The given figure shows a small mass connected to a string, which is attached to a vertical post. If the mass is released from rest when the string is horizontal as shown, the magnitude of the total acceleration of the mass as a function of the angle $\theta$ is

• A. $2\, g\, \sin \theta$
• B. $2\, g\, \cos \theta$
• C. $g\sqrt{3\, \cos^{2} \theta+1}$
• D. $g\sqrt{3\, \sin^{2} \theta+1} $

Answer 1

Answer: (D)

From conservation of energy $\Delta K+\Delta U=0$
$m g h=\frac{1}{2} m v^{2} m g l \sin \theta$
$=\frac{1}{2} m v^{2}$
$\Rightarrow a_{C}=2 g \sin \theta=\frac{v^{2}}{l}=$ radial acceleration
$g \cos \theta=a_{t}=$ tangential acceleration

Total acceleration
$a=\sqrt{a_{c}^{2}+a_{t}^{2}}$
$=g \sqrt{\cos ^{2} \theta+(2 \sin \theta)^{2}}$
$=g \sqrt{\left(1-\sin ^{2} \theta\right)+4 \sin ^{2} \theta}$
$=g \sqrt{1+3 \sin ^{2} \theta}$