Q.
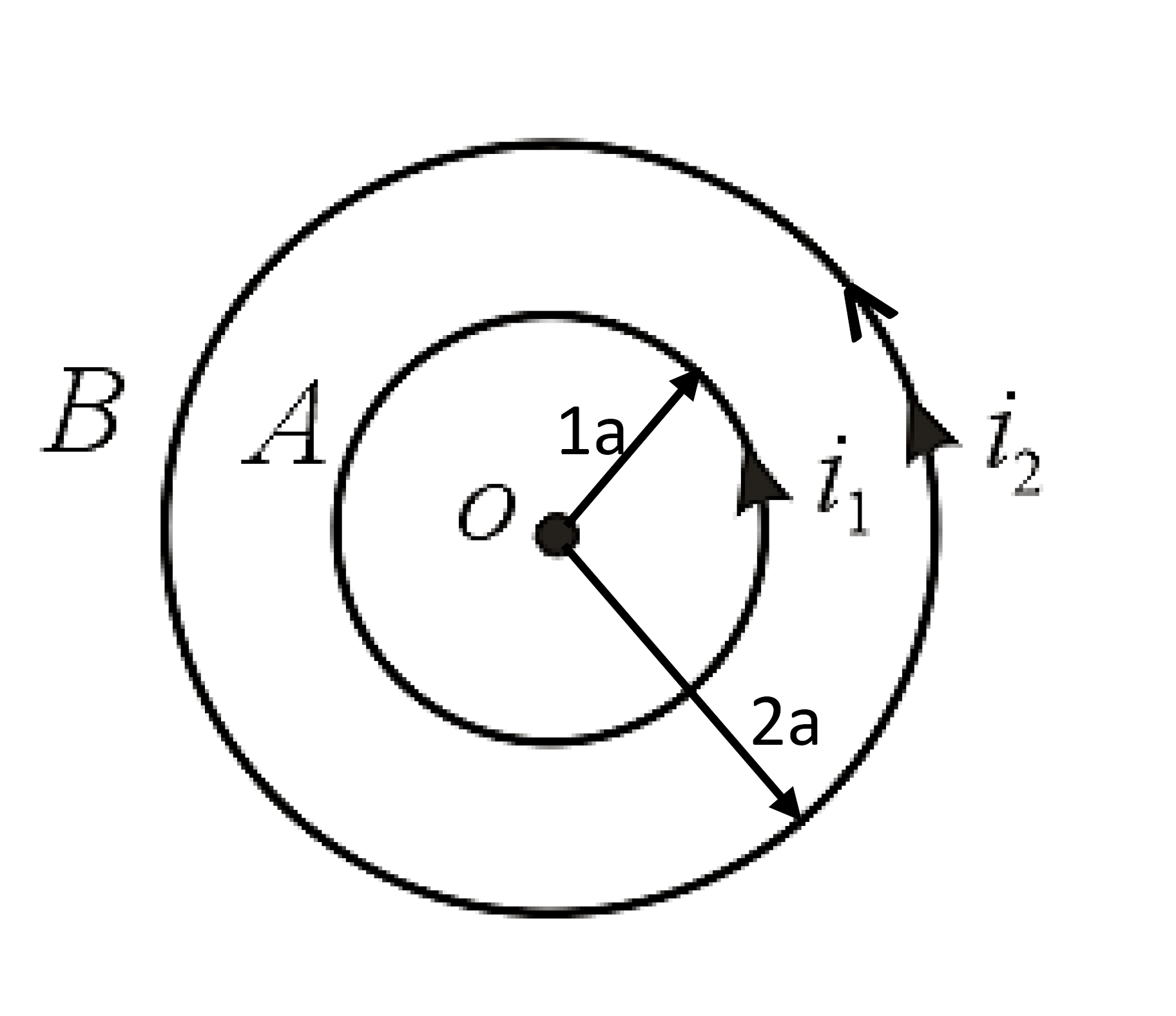
The given diagram shows $A$ and $B$ which are two concentric circular conductors having the common centre $O$ . These conductors carry currents $i_{1}$ and $i_{2}$ , respectively and ratio of their radii is $1:2$ . If the ratio of the flux densities at $O$ due to $A$ and $B$ is $1:3$ , then calculate the value of the ratio of their respective currents, i.e., $\frac{i_{1}}{i_{2}}$ .
NTA AbhyasNTA Abhyas 2020
Solution:
Magnetic field at the centre of circular coil is given by
$B=\frac{\mu _{0} I}{2 r}$
$B \propto \frac{I}{r}$
$\Rightarrow B_{A} \propto \frac{I_{1}}{r_{1}}$
$\Rightarrow B_{B} \propto \frac{I_{2}}{r_{2}}$
$\Rightarrow \frac{B_{A}}{B_{B}}=\frac{I_{1}}{I_{2}}\times \frac{2 r}{r}$
$\Rightarrow \frac{1}{3}=\frac{I_{1}}{I_{2}}\times 2$
$\Rightarrow \frac{I_{1}}{I_{2}}=\frac{1}{6}$
Magnetic field at the centre of circular coil is given by
$B=\frac{\mu _{0} I}{2 r}$
$B \propto \frac{I}{r}$
$\Rightarrow B_{A} \propto \frac{I_{1}}{r_{1}}$
$\Rightarrow B_{B} \propto \frac{I_{2}}{r_{2}}$
$\Rightarrow \frac{B_{A}}{B_{B}}=\frac{I_{1}}{I_{2}}\times \frac{2 r}{r}$
$\Rightarrow \frac{1}{3}=\frac{I_{1}}{I_{2}}\times 2$
$\Rightarrow \frac{I_{1}}{I_{2}}=\frac{1}{6}$