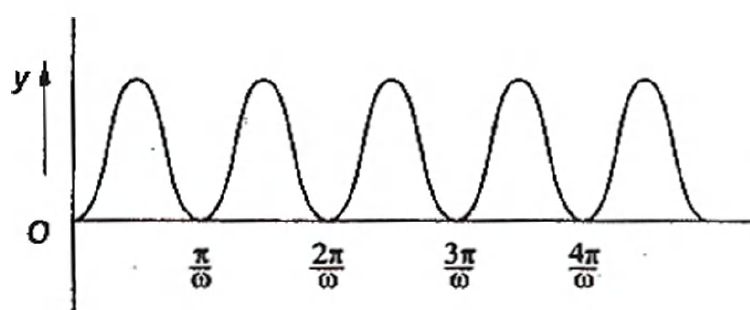
Question

The function $sin^2 \,(\omega t)$ represents :

• A. a periodic, but not simple harmonic, motion with a period $2\pi/\omega$
• B. a periodic, but not simple harmonic, motion with a period $\pi/\omega$
• C. a simple harmonic motion with a period $2\pi/\omega$
• D. a simple harmonic motion with a period $\pi/\omega$

Answer 1

Answer: (B)

Here, $y - sin^2\, \omega t$
$\frac{dy}{dt}=2\,\omega\,sin\,cos\,\omega\,t=\omega\,2\,\omega t$
$\frac{d^{2}y}{dt^{2}}=2\,\omega^{2}\,cos\,2\,\omega t$
For SHM, $\frac{d^{2}y}{dt^{2}}\,\propto-y$
Hence, function is not $SHM$, but periodic. From the $y-t$ graph, time period is
$T=\frac{\pi}{\omega}$