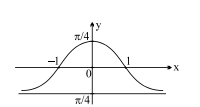
Question

The function $f(x)=\tan ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)$ is

• A. increasing in its domain
• B. decreasing in its domain
• C. decreasing in $(-\infty, 0)$ and increasing in $(0, \infty)$
• D. increasing in $(-\infty, 0)$ and decreasing in $(0, \infty)$

Answer 1

Answer: (D)

put $\mathrm{x}^{2}=\tan \theta$ to get
$f(x)=\frac{\pi}{4}-\tan ^{-1}\left(x^{2}\right)$
$\Rightarrow \mathrm{f}^{\prime}(\mathrm{x})=-\frac{2 \mathrm{x}}{1+\mathrm{x}^{4}}$ which is greater than zero for $\mathrm{x}<0$ and less than zero for $\mathrm{x}>0$
$\Rightarrow (\mathrm{D})]$