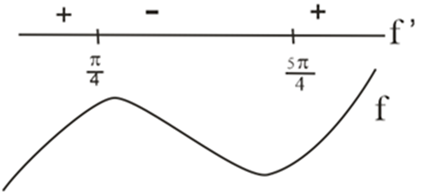
Question

The function $f\left(x\right)=e^{sin x + cos ⁡ x}$ $\forall x\in \left[0 , 2 \pi \right]$ attains local extrema at $x=\alpha $ and $x=\beta ,$ then $\alpha +\beta $ is equal to

• A. $\pi $
• B. $2\pi $
• C. $\frac{3 \pi }{2}$
• D. $\frac{\pi }{2}$

Answer 1

Answer: (C)

$f^{'} \left(x\right) = e^{sin x + cos x} \cdot \left(cos x - sin x\right)$

$\therefore f\left(x\right)$ attains local extrema at $x=\frac{\pi }{4},\frac{5 \pi }{4}$
i.e. $\alpha +\beta =\frac{6 \pi }{4}=\frac{3 \pi }{2}$