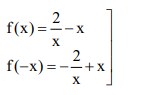Question

The function $f$ is not defined for $x =0$, but for all non zero real numbers $x$, $f(x)+2 f\left(\frac{1}{x}\right)=3 x$. The equation $f(x)=f(-x)$ is satisfied by

• A. exactly one real number
• B. exactly two real numbers
• C. no real numbers
• D. all non zero real numbers.

Answer 1

Answer: (B)

$f ( x )+2 f \left(\frac{1}{ x }\right)=3 x$....(1)
$x \rightarrow \frac{1}{x}, \quad 2 f(x)+f\left(\frac{1}{x}\right)=\frac{3}{x}$....(2)
or $4 f(x)+2 f\left(\frac{1}{x}\right)=\frac{6}{x}$(3)
(3) -(1)
$3 f(x)=\frac{6}{x}-3 x$

now $f ( x ) = f (- x ) $
$ \frac{2}{ x }- x =-\frac{2}{ x }+ x \Rightarrow \frac{4}{ x }=2 x$
$ \Rightarrow x ^2=2 \Rightarrow x =\sqrt{2} \text { or }-\sqrt{2} \Rightarrow(B)$