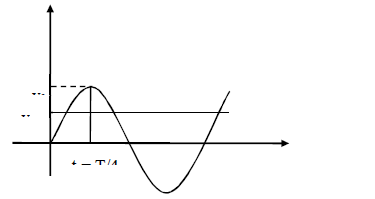
Q. The frequency of an alternating current is 50 Hz. What is the minimum time taken by current to reach its peak value from rms value?
Solution:
We know that $V_{rms}=V_{0} \, sin \, \omega t$
$\frac{V_{0}}{\sqrt{2}}=V_{0} sin\, \omega t$
$\therefore \, sin \, \omega t=\left(\frac{1}{\sqrt{2}}\right)$
$i.e., \omega t=\frac{\pi}{4} \Rightarrow \frac{2 \pi}{T}. t=\frac{\pi}{4}$
$\therefore \, t=\frac{T}{8}$
Time for current to reach from rms value to peak value is i.e.,$ l_{rms} \rightarrow l_{0}$
$\frac{T}{4}-\frac{T}{8}=\frac{T}{8} \quad\left(\frac{I_{0}}{\sqrt{2}}\to I_{0}\right)$
$f=50 \quad\therefore \, t=\frac{I}{8}$
$=\frac{1}{50\times8}=\frac{1}{400}=0.25\times10^{-2}$
$=2.5\times10^{-3} sec \, \therefore \, \left[D\right] is\, correct.$