Question

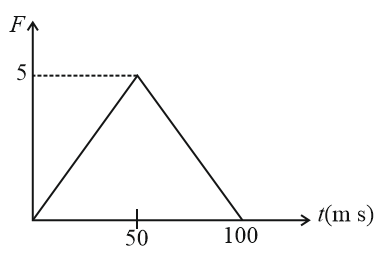
The force vs time graph of an object of mass $1\,kg$ which is initially at rest is shown below. What will be the graph of momentum vs time for the given graph?

• A.
• B.
• C.
• D.

Answer 1

Answer: (A)

$\Delta \vec{P}=\int \vec{F}dt$
For $t\leq 0.05\,s,F=\frac{5}{0 .05}t\Rightarrow F=100t$
For $0.05s\leq t\leq 0.1s,F=-100t+10$
For $0$ to $0.05 \,s$,
$P_{2}-P_{1}=\int \limits_{0}^{0 .05}100tdt\Rightarrow P_{2}=100\left(\frac{0 . \left(05\right)^{2}}{2}\right)$
$\Rightarrow P_{2}=50\times \left(\frac{1}{20}\right)^{2}\Rightarrow P_{2}=\frac{50}{400}$
$\Rightarrow P_{2}=\frac{1}{8}\Rightarrow P_{2}=0.125\,Ns$
For $0.05 \,s$ to $0.1\, s$,
$P_{2}-0.125=\int\limits _{0 .05}^{0 .1}\left(- 100 t + 10\right)dt$
$\Rightarrow P_{2}-0.125=\left[- 100 \left(\frac{t^{2}}{2}\right) + 10 t\right]_{0 . 05}^{0 . 1}$
$\Rightarrow P_{2}-0.125=-50\left[\frac{1}{100} - \frac{1}{400}\right]+10\left[\frac{1}{10} - \frac{1}{20}\right]$
$\Rightarrow P_{2}-0.125=-50\left[\frac{4 - 1}{400}\right]+\frac{1}{2}$
$\Rightarrow P_{2}-0.125=-50\times \frac{3}{400}+\frac{1}{2}$
$\Rightarrow P_{2}-0.125=-\frac{3}{8}+\frac{1}{2}$
$\Rightarrow P_{2}-0.125=\frac{- 3 + 4}{8}$
$\Rightarrow P_{2}-0.125=0.125\Rightarrow P_{2}=0.25\,kg\,ms^{- 1}$