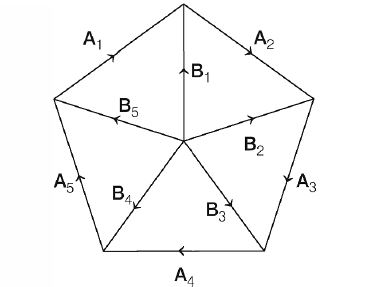
Question

The five sides of a regular pentagon are represented by vectors $A_{1},A_{2},A_{S},A_{4}$ and $A_{5},$ in cyclic order as shown below

Corresponding vertices are represented by $B_{1}, B_{2},B_{3} ,B_{4} $ and $B_{5}$, drawn from the centre of the pentagon.
Then, $B_{2} + B_{3} + B_{4} + B_{5}$ is equal to

• A. $A_{1}$
• B. $-A_1$
• C. $B_1$
• D. $-B_1$

Answer 1

Answer: (D)

From triangle law, in given vector pentagon,

We have
$B_{2}+A_{3}=B_{3} \, . . . (i)$
$B_{3}+A_{4}=B_{4} \, . . . (ii)$
$B_{4}+A_{5}=B_{5} \, . . . (iii)$
$B_{5}+A_{1}=B_{1} \, . . . (iV)$
Adding these equations, we have
$\Rightarrow (B_{2} +B_{3} +B_{4} +B_{5})$
$+(A_{3} + A_{4} + A_{5} + A_{4})$
$= (B_{3} + B_{4} + B_{5} + B_{4})$
$\Rightarrow ( B_{2} + B_{3} + B_{4},+ B_{5} +$
$(- A_{2}) = (- B_{2}) ...(v )$
As from polygon law of vector addition
$A_{3} + A_{4} + A_{5} + A_{1} = - A_{2}$
and $B_{3} + B_{4} + B_{5} + B_{1} = - B_{2}$
So, from Eq. (v), we have
$B_{2} + B_{3} +B_{4}+B_{5}$
$ = A_{2} -B_{2}=-B_{1}$