Q.
The figure shows two solid discs with radius $R$ and $r$ respectively. If mass per unit area is same for both, what is the ratio of $MI$ of bigger disc around axis $AB$ (Which is $\perp$ to the plane of the disc and passing through its centre) of MI of smaller disc around one of its diameters lying on its plane?
Given ' $M$ ' is the mass of the larger disc. ($MI$ stands for moment of inertia)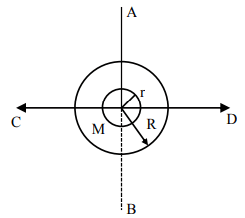
Solution: