Q.
The figure shows the plot of velocity $(v)$ versus time $(t)$ on a log-log scale. Assuming straight line motion and the particle to start from origin, the distance (in metre) covered at the end of $t=3\, s$ is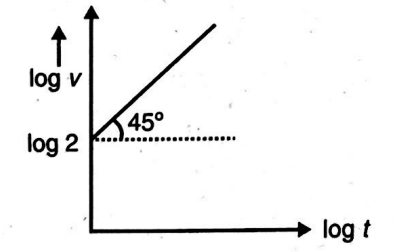
Motion in a Straight Line
Solution: