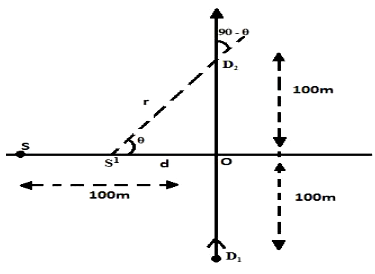
Question

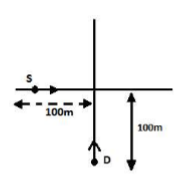
The figure shows the location of a source and detector at time $t=0$ . The source and detector are moving with velocities $v_{S}=5\hat{i}$ $m \, s^{- 1}$ and $v_{D}=10\hat{j}$ $m \, s^{- 1}$ respectively. The frequency of signals received by the detector at the moment when the source crosses the origin is (the frequency of the source is 100 Hz. velocity of sound $330 \, m \, s^{- 1}$ )

• A. $97Hz$
• B. $47Hz$
• C. $90Hz$
• D. $60Hz$

Answer 1

Answer: (A)

Time taken by 'S' to travel from S to 0 = $20s$
In this time detector goes from $D_{1}$ to $D_{2}$
The signal received by the detector at $t=20s$ is not that produced by the source at 'O' but produced from a position $S_{1}$ prior to 'O'
$\frac{r}{v}=\frac{d}{v_{s}}cos \theta =\frac{d}{r}=\frac{v_{s}}{v}=\frac{5}{330}=\frac{1}{66}$
$sin \theta = \sqrt{1 - \left(\right. \frac{1}{66} \left.\right)^{2}} \approx 1$
$\Rightarrow f_{D}=f\left(\frac{v - v_{0} sin \theta }{v - v_{s} cos ⁡ \theta }\right)$
$=100\left(\frac{330 - 10}{330 - \frac{5}{66}}\right)=97 \, Hz$