Q.
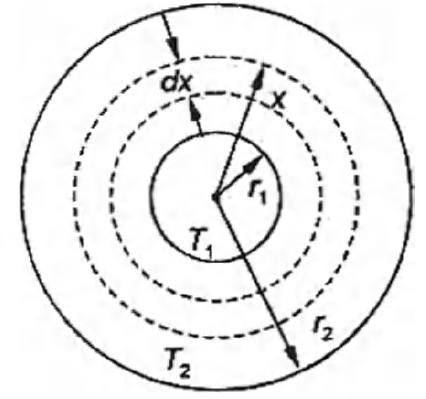
The figure shows a system of two concentric spheres of radii $r_1$, and $r_2$ and kept at temperatures $T_1$ and $T_2$, respectively. The radial rate of flow of heat in a substance between the two concentric spheres, is proportional to :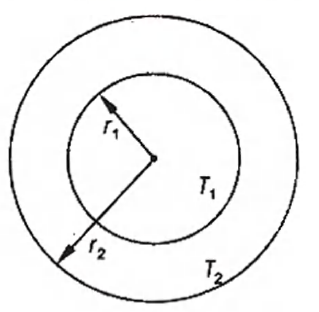
AIEEEAIEEE 2005Thermal Properties of Matter
Solution:
To measure the radial rate of heat flow, we have to go for integration technique as here the area of the surface through which heat will flow is not constant.
Let us consider an element (spherical shell) of thickness $dx$ and radius $x$ as shown in figure. Let us first find the equivalent thermal resistance between inner and outer sphere.
Resistance of shell $=dR=\frac{dx}{K\times4\pi x^{2}}$
$\begin{bmatrix}from\,R=\frac{1}{KA}\,where\\ K \rightarrow thermal\, conductivity\end{bmatrix}$
$\Rightarrow \int\,dR=R=\int ^{r_{2}}_{r_1} \frac{dx}{4\pi\,Kx^{2}}=\frac{1}{4\pi\,K}\left[\frac{1}{r_{1}}-\frac{1}{r_{2}}\right]$
$=\frac{r_{2}-r_{1}}{4\pi\,K\,\left(r_{1}r_{2}\right)}$
Rate of heat flow $= H$
$=\frac{T_{1}-T_{2}}{R}= \frac{T_{1}-T_{2}}{r_{2}-r_{1}}\times 4\pi K\left(r_{1}r_{2}\right) \propto \frac{r_{1}r_{2}}{r_{2}-r_{1}}$