Q.
The figure shows a system consisting of (i) a ring of outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed $\omega$ and (ii) an inner disc of radius 2R rotating anti-clockwise with angular speed $\omega /2$. The ring and disc are separated by frictionless ball bearings. The system is in the x-z plane. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of $30^{\circ}$ with the horizontal. Then with respect to the horizontal surface,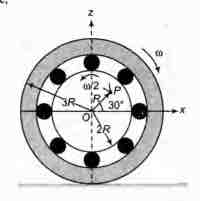
IIT JEEIIT JEE 2002System of Particles and Rotational Motion
Solution:
Velocity of point $O$ is
$v_{0}=(3 r \omega) \hat{i}$
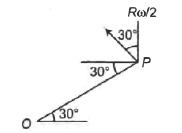
$v_{P O}$ is $\frac{R . \omega}{2}$ in the direction shown in figure.
In vector form
$V_{P O}=-\frac{R \omega}{4} \sin 30^{\circ} \hat{i}+\frac{R \omega}{2} \cos 30^{\circ} \hat{k}$
$V_{P O}=-\frac{R \omega}{4} \sin 30^{\circ} \hat{i}$
$=-\frac{R \omega}{4} \hat{i}+\frac{\sqrt{3} R \omega}{4} \hat{k}$
But $V_{P O}=v_{P}-v_{O}$
$\therefore V_{P}=v_{P O}-v_{O}$
$=\left(-\frac{R \omega}{4} \hat{i}+\frac{\sqrt{3} R \omega}{4} \hat{k}\right)+3 R \omega \hat{i}$
$=\frac{11}{4} R \omega \hat{i}+\frac{\sqrt{3}}{4} R \omega \hat{k}$