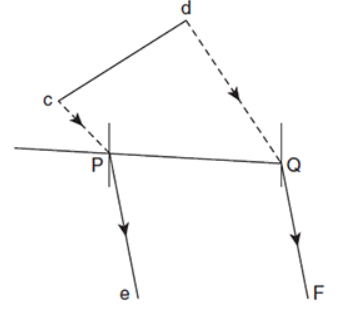
Question

The figure shows a surface $X Y$ separating two transparent media, medium-$1$ and medium-$2$. The lines $ab$ and $cd$ represent wave fronts of a light wave traveling in medium-$1$ and incident on $X Y$. The lines $ef$ and $gh$ represent wave fronts of the light wave in medium-$2$ after refraction.

The phases of the light wave at c, $d$, e and $f$ are $\phi_{c}, \phi_{d}, \phi_{e}$ and $\phi_{f}$, respectively. It is given that $\phi_{c} \neq \phi_{f}$.

• A. $\phi_{c}$ cannot be equal to $\phi_{d}$
• B. $\phi_{d}$ can be equal to $\phi_{e}$
• C. $\left(\phi_{d}-\phi_{f}\right)$ is equal to $\left(f_{c}-\phi_{e}\right)$
• D. $\left(\phi_{d}-\phi_{c}\right)$ is not equal to $\left(\phi_{f}-\phi_{e}\right)$

Answer 1

Answer: (C)

Optical path length is same for the lines $df$ and $ce$ and hence the phase change is also same:

We have $\left.\phi_{d}-\phi\right) f=\phi_{c}-\phi_{e}$
as $t_{d Q}+t_{Q f}=t_{c P}+t_{P e}$.
We know that $Y$ remains unchanged in both media (denser and rarer).
Therefore,
$\gamma t_{d Q}+\gamma t_{Q f}=\gamma t_{c P}+\gamma t_{P e}$
That is,
$\left(\frac{V_{1}}{\lambda_{1}}\right) t_{d Q}+\left(\frac{V_{2}}{\lambda_{2}}\right) t_{Q f}=\left(\frac{V_{1}}{\lambda_{1}}\right) t_{c P}+\left(\frac{V_{2}}{\lambda_{2}}\right) t_{P e}$
$\frac{d Q}{\lambda_{1}}+\frac{Q f}{\lambda_{2}}=\frac{c P}{\lambda_{1}}+\frac{P e}{\lambda_{2}} $
$\frac{d Q-c P}{\lambda_{1}}=\frac{P e-Q f}{\lambda_{2}} $
$\frac{2 \pi}{\lambda_{1}}(d Q-c P)=\frac{2 \pi}{\lambda_{2}}(P e-Q f)$
$\Rightarrow \phi_{d}-\phi_{c}=\phi_{c}-\phi_{f}(1)$
Since all points on a wave front are at the same phase, we have
$\phi_{d}=\phi_{c}$ and $\phi_{f}=\phi_{e}(2)$
Here, from (1) and (2),
$\left(\phi_{d}-\phi_{f}\right)$ is equal to $\left(\phi_{c}-\phi_{e}\right)$.