Question

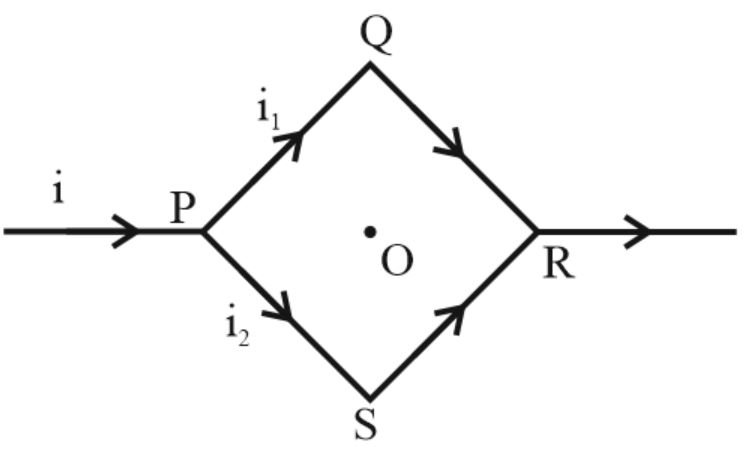
The figure shows a square loop $ \, PQRS$ with an edge length $a$ . The resistance of the wire $PQR$ is $r$ and that of $PSR$ is $2r$ . The value of the magnetic field at the centre of the loop is found to be $\frac{\sqrt{2} \mu _{0} i}{k \pi a}$ , then what is the value of $k$ ?

Answer 1

The magnetic field due to a straight current-carrying wire is
$B=\frac{\mu _{0} I}{4 \pi d}\left[sin \alpha + sin \beta \right]$
$B_{\mathrm{PQR}}=2 \times \frac{\mu_0\left(\frac{2 i}{3}\right)}{4 \pi\left(\frac{a}{2}\right)}\left[\sin 45^{\circ}+\sin 45^{\circ}\right]$
$B_{\mathrm{PSR}}=2 \times \frac{\mu_0\left(\frac{i}{3}\right)}{4 \pi\left(\frac{a}{2}\right)}\left[\sin 45^{\circ}+\sin 45^{\circ}\right]$
$B_{net}=B_{PQR}-B_{PSR}$
$\Rightarrow B_{net}=\frac{\sqrt{2} \mu _{0} i}{3 \pi a}$
$\Rightarrow k=3$