Question

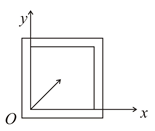
The figure shows a square carrom board without any pockets. A coin is pushed from the corner, which is the origin, with a velocity $\overset{ \rightarrow }{v}=\left(\right.2\hat{i}+3\hat{j}\left.\right)$ . Assume gravity and friction to be absent. The coin collides with edges of the carrom board elastically. What is the velocity vector of coin after the $3^{\text{rd}}$ collision ?

• A. $2\hat{i}+3\hat{j}$
• B. $2\hat{i}-3\hat{j}$
• C. $-2\hat{i}+3\hat{j}$
• D. $-2\hat{i}-3\hat{j}$

Answer 1

Answer: (C)

After each collision normal components of velocity gets reversed.
$\therefore $ after $1^{\text{st}}$ collision, velocity of coin, $\overset{ \rightarrow }{v}_{1}=2\hat{i}-3\hat{j}$
after $2^{\text{st }}$ collision, velocity of coin, $\overset{ \rightarrow }{v}_{2}=-2\hat{i}-3\hat{j}$
after $3^{\text{rd }}$ collision, velocity of coin, $\overset{ \rightarrow }{v}_{3}=-2\hat{i}+3\hat{j}$