Question

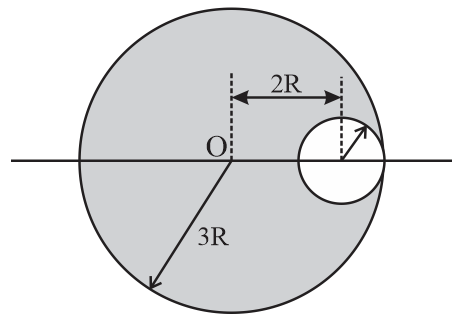
The figure shows a disc of radius $3R$ from which a circular hole of radius $R$ is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point $O$ is

• A. $R/4$
• B. $R/5$
• C. $R/3$
• D. $R/6$

Answer 1

Answer: (A)

The centre of mass of the remaining object is
$x_{cm}=\frac{m_{1} x_{1} - m_{2} x_{2}}{m_{1} - m_{2}}=\frac{\sigma A_{1} x_{1} - \sigma A_{2} x_{2}}{\sigma A_{1} - \sigma A_{2}}$
where $m_{1}$ and $A_{1}$ are the mass and area of the total disc and $m_{2}$ and $A_{2}$ are the mass and area of the cut-out portion. $\sigma $ is the mass per unit length of the disc.
$A_{1}=\pi (3R^{2}$ , $A_{2}=\pi R^{2}$
$x_{1}=0$ , $x_{2}=2R$
$\Rightarrow x_{cm}=-R/4$