Question

The figure shows a circular loop of radius $a$ with two long parallel wires (numbered 1 and 2 ) all in the plane of the paper. The distance of each wire from the centre of the loop is $d$. The loop and the wires are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.

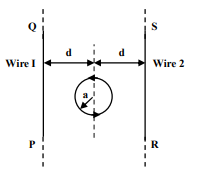
When $d \approx a$ but wires are not touching the loop, it is found that the net magnetic field on the axis of the loop is zero at a height $h$ above the loop. In that case

• A. current in wire 1 and wire 2 is the direction PQ and $R S$, respectively and $h \approx a$
• B. current in wire 1 and wire 2 is the direction $P Q$ and $S R$, respectively and $h \approx a$
• C. current in wire 1 and wire 2 is the direction $P Q$ and $S R$, respectively and $h \approx 1.2 a$
• D. current in wire 1 and wire 2 is the direction $P Q$ and $R S$, respectively and $h \approx 1.2 a$

Answer 1

Answer: (C)

The net magnetic field at the given point will be zero if.
$\left|\vec{ B }_{\text {wires }}\right|=\left|\vec{ B }_{\text{loop }}\right| $
$\Rightarrow 2 \frac{\mu_{0} I }{2 \pi \sqrt{ a ^{2}+ h ^{2}}} \times \frac{ a }{\sqrt{ a ^{2}+ h ^{2}}} $
$=\frac{\mu_{0} Ia ^{2}}{2\left( a ^{2}+ h ^{2}\right)^{3 / 2}}$
$\Rightarrow h \approx 1.2 a$
The direction of magnetic field at the given point due to the loop is normally out of the plane. Therefore, the net magnetic field due the both wires should be into the plane. For this current in wire I should be along $PQ$ and that in wire $RS$ should be along $SR$.