Q.
The figure shows a block placed on a bracket. The bracket is placed unconstrained on a smooth floor and is pulled by a constant force $\vec{F}=6 \hat{i}$ horizontally. The block is projected with velocity $v_{0}$ relative to the bracket as shown in the figure. If the time (in second) after which it stops relative to bracket is $t$, then find the value of $0.6\,t$ Horizontal surface of bracket is smooth while vertical surface is rough.
(Given: $m=1 \,kg , M=5\, kg , v_{0}=5 \,m / s , \mu=0.5$ )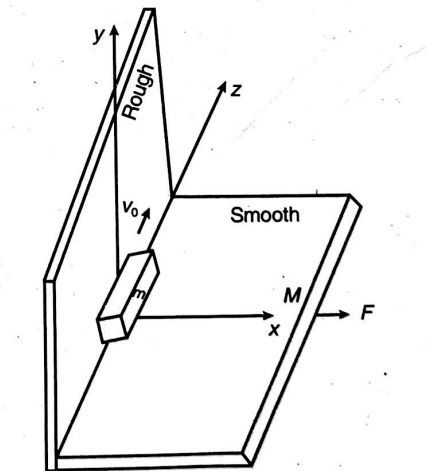
Laws of Motion
Solution: