Question

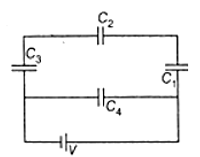
The figure given below shows a network of four capacitors of capacitance equal to $C_{1}=C, \, C_{2}=2C, \, C_{3}=3C, \, C_{4}=4C$ are connected to a battery. If the ratio of charges on $C_{2} \, and \, C_{4}$ is $\frac{p}{q}$ then what is the value of $\left(p + q\right)$ , where $p$ and $q$ are smallest positive integers.

Answer 1

The charge flowing through $C_{4}$ is
$q_{4}=C_{4}\times V=4 \, C_{V}$
The series combination of $C_{1}, \, C_{2} \, and \, C_{3}$
$\frac{1}{C^{′}}=\frac{1}{C}+\frac{1}{2 C}+\frac{1}{3 C}$
$\frac{1}{C^{′}}=\frac{6 + 3 + 2}{6 C}=\frac{11}{6 C}\Rightarrow C^{′}=\frac{6 C}{11}$
Now, $C^{′} \, and \, C_{4}$ form parallel combination giving
$C " = C ′ + C_{4}=\frac{6 C}{11}+4C=\frac{50 C}{11}$
Net Charge, $q=C"V=\frac{50}{11}CV \, $
$q^{′}=q-q_{4}=\frac{50}{11} \, CV-4CV=\frac{6 C V}{11}$
Total Charge flowing through $C_{1},C_{2}$ and $C_{3}$ will be
$q^{′}=q-q_{4}=\frac{50}{11}CV-4CV=\frac{6 C V}{11}$
Since, $C_{1}, \, C_{2}, \, C_{3}$ are in series combination. Hence, charge flowing through these will be same
Hence, $q_{2}=q_{1}=q_{3}=q^{′}=\frac{6 \, C V}{11}$
Thus, $\frac{q_{2}}{q_{4}}=\frac{\frac{6 \, C V}{11}}{4 \, C V}=\frac{3}{22}$