Q.
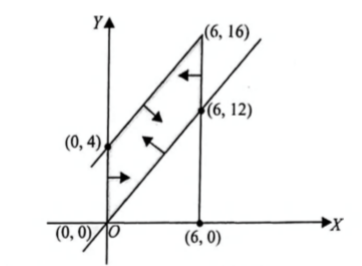
The feasible region for an $LPP$ is shown shaded in the figure.
Let $F = 3x - 4y $ be the objective function. Maximum value of $F$ is
Linear Programming
Solution:
The fesible region as shown in the figure, has
objective function $F = 3x - 4y$.
Corner Points
Corresponding value of $F = 3x - 4y$
(0,0)
0
(12, 6)
12 (maximum)
(0, 4)
-16 (Minimum)
Hence, the maximum value of $F$ is $12$.
| Corner Points | Corresponding value of $F = 3x - 4y$ |
|---|---|
| (0,0) | 0 |
| (12, 6) | 12 (maximum) |
| (0, 4) | -16 (Minimum) |