Q.
The feasible region for an LPP is shown below. If $Z=4 x+y$, then the minimum value of $Z$ is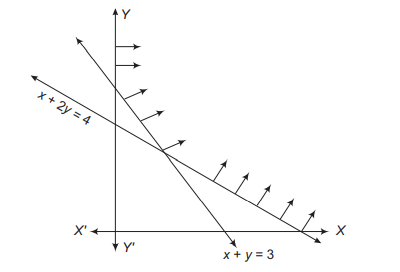
Linear Programming
Solution:
The given feasible region is
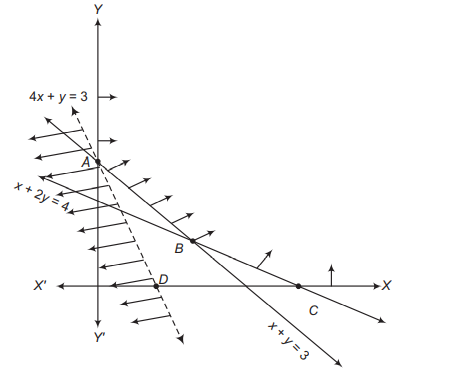
From the above graph, we see that $A B C$ is the feasible region which is unbounded and its corner points are $A(0,3), B(2,1), C(4,0)$.
The given objective function is $Z=4 x+y$
The values of $Z$ at the corner points are given by
Corner point
Corresponding value of $Z$
$(0,3)$
3
$(2,1)$
9
$(4,0)$
16
From the above table, we see that the minimum value of $Z$ is
3 . Now, to check, if $Z=3$ is the minimum value, we draw the line $4 x+y=3$
Since, the open half plane $4 x+y<3$ does not intersect the feasible region at any point. Hence, minimum value of $Z$ is 3.
| Corner point | Corresponding value of $Z$ |
|---|---|
| $(0,3)$ | 3 |
| $(2,1)$ | 9 |
| $(4,0)$ | 16 |