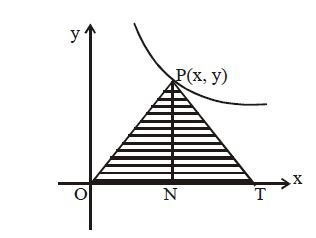
Q. The family of curves for which the area of the triangle formed by the x-axis, the tangent drawn at any point on the curve and radius vector of the point of tangency is constant equal to $2a^2$, is given by
Differential Equations
Solution:
Tangent drawn at any point P (x, y) is
$Y - y = \frac{dy}{dx}\left(X-x\right)\quad...\left(i\right)$
The triangle , whose area is given is $_{\Delta} OPT$ (see the shaded region in the adjacent figure) If coordinates of T are $\left(X, 0\right)$ then

$X = x - y \frac{dx}{dy}$ (Put $Y = 0$ in $\left(i\right)$) $\quad\therefore $ area of $_{\Delta } OPT$
$= \frac{1}{2} \left|X\cdot y\right| = 2a^{2} \quad$ (given)
$\therefore \frac{1}{2}\left|xy-y^{2} \frac{dx}{dy}\right| = 2a^{2} \Rightarrow xy - y^{2} \frac{dx}{dy} = \pm2a^{2}$
$\Rightarrow \frac{dx}{dy} -\frac{x}{y} = \pm \frac{2a^{2}}{y^{2}}$, which is linear in x
The integrating factor is $I.F. = e^{\int-\frac{1}{y}dy} e ^{-log y } = \frac{1}{y}$
The solution is $x\left(\frac{1}{y}\right) = \int \pm \frac{2a^{2}}{y^{2}}\left(\frac{1}{y}\right)dy + c$
$\Rightarrow \frac{x}{y} = \pm \frac{2a^{2}y^{-2}}{-2} + \Rightarrow x = cy \pm \frac{a^{2}}{y}$