Question

The expression $y=a x^2+b x+c(a, b, c \in R$ and $a \neq 0)$ represents a parabola which cuts the $x$-axis at the points which are roots of the equation $ax ^2+ bx + c =0$. Column-II contains values which correspond to the nature of roots mentioned in column-I.

Column I		Column II
A	For $a =1, c =4$, if both roots are greater than 2 then $b$ can be equal to	P	4
B	For $a =-1, b =5$, if roots lie on either side of -1 then $c$ can be equal to	Q	8
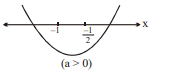
C	For $b=6, c=1$, if one root is less than -1 and the other root greater than (	R	10$\frac{-1}{2}$ then a can be equal to
		S	no real value

• A. (A) S (B) Q, R (C) P
• B. (A) S (B) Q, R (C) Q
• C. (A) S (B) Q, R (C) R
• D. (A) S (B) Q, R (C) S

Answer 1

Answer: (A)

(A) We have $f(x)=x^2+b x+4$
$\therefore D \geq 0 \Rightarrow b^2-16>0 \Rightarrow b \in(-\infty,-4] \cup[4, \infty) $
$\text { and } f(2)>0 \Rightarrow 4+2 b+4>0 \Rightarrow b>-4$
Also $2<\frac{-b}{2} \Rightarrow 4<-b \Rightarrow b<-4$.

Hence $b \in \phi$.
(B) We have $f(x)=-x^2+5 x+c$
Clearly $f (-1)>0 \Rightarrow-1-5+ c >0$
Hence $c >6$.

(C) We have $f(x)=a x^2+6 x+1$
Now $D >0 \Rightarrow 36-4 a >0 \Rightarrow a <9$
Case-I : If $a >0, f (-1)<0 \Rightarrow a -6+1<0 \Rightarrow a <5$.
and $ f \left(\frac{-1}{2}\right)<0 \Rightarrow \frac{ a }{4}-3+1<0 \Rightarrow a <8$.

Hence $a \in(0,5)$
Case-II : If $a <0, f (-1)>0$ and $f \left(\frac{-1}{2}\right)>0$

$\Rightarrow a -6+1>0 \text { and } \frac{ a }{4}-3+1>0 \Rightarrow a >5 \text { and } \frac{ a }{4}>2 $
$\therefore a >8 \text { (Rejected) }$
Hence we conclude from case-I and case-II that $a \in(0,5)]$