Q.
The equivalent resistance of the arrangement of resistances shown in the given figure between points $P$ and $Q$ is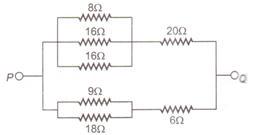
AMUAMU 2004
Solution:
In the given circuit, the three resistors of $3\, \Omega,\, 16\, \Omega$ and $16\, \Omega$ are connected in parallel, hence equivalent resistance is
$\Rightarrow R'=4\, \Omega$
This $4\, \Omega$ resistor is connected in series with $20\, \Omega$ resistor.
$R''=20\, \Omega+4\, \Omega=24\, \Omega$
Similarly in the lower arm, the $9\, \Omega$ and $18\, \Omega$ resistance's are connected in parallel, hence equivalent resistance is
$\frac{1}{R'''} =\frac{1}{9}+\frac{1}{18}=\frac{18+9}{18 \times 9}$
$\Rightarrow R'''=6\, \Omega$
The two $6 \,\Omega$ resistor's are connected in series, hence equivalent resistance is
$R'''=6\, \Omega+6 \,\Omega=12\, \Omega$
Resultant equivalent resistance between $P$ and $Q$ is
$\frac{1}{R} =\frac{1}{24} +\frac{1}{12}$
$\Rightarrow R =8\, \Omega$