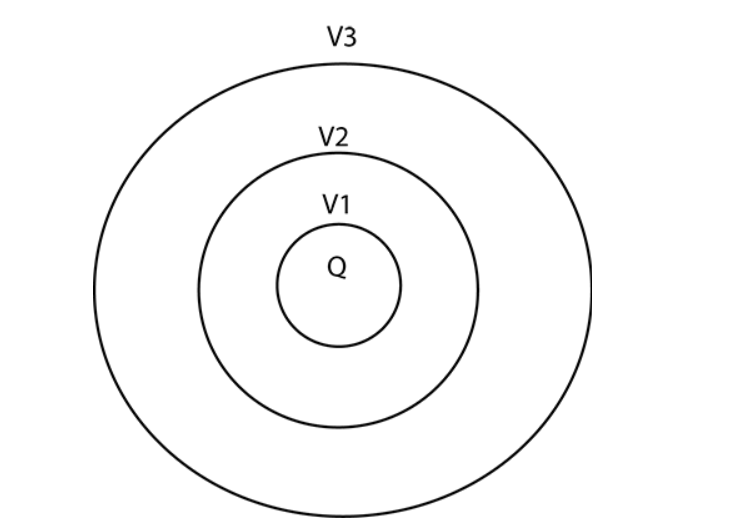
Question

The equipotential surfaces corresponding to bsingle positive charge are concentric spherical shells with the charge at its origin. The spacing between the surfaces for the same change in potential

• A. is uniform throughout the field
• B. is getting closer as r $\rightarrow \infty$
• C. is getting closer as $\rightarrow 0$
• D. can be.varied as one wishes to

Answer 1

Answer: (C)

Let the equipotential surfaces have potential $V _{1}, V _{2}, V _{3}$ with, $V _{1}> V _{2}> V _{3}$
Also, let $V_{3}-V_{2}=V_{2}-V_{1}=R$
Potential of a charge is given by $kQ / r$
$V = kQ / r \Rightarrow r = kQ / V$
Distance between the equipotential surfaces is
$kQ \left(\frac{1}{ V _{2}}-\frac{1}{ V _{3}}\right) \text { and } kQ \left(\frac{1}{ V _{1}}-\frac{1}{ V _{2}}\right)$
or
$kQ \left(\frac{ V _{3}- V _{2}}{ V _{3} V _{2}}\right)$ and $kQ \left(\frac{ V _{2}- V _{1}}{ V _{2} V _{1}}\right)$
or
$kQ \left(\frac{ R }{ V _{3} V _{2}}\right)$ and $kQ \left(\frac{ R }{ V _{2} V _{1}}\right)$
Clearly $V _{2} V _{1}> V _{3} V _{2}$
Thus
$kQ \left(\frac{ R }{ V _{3} V _{2}}\right)> kQ \left(\frac{ R }{ V _{2} V _{1}}\right)$
Therefore spacing between surfaces decreases as potential increases i.e. $r$ decreases.