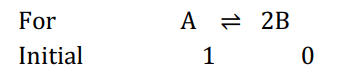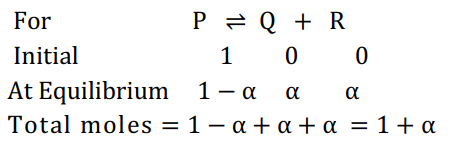Question

The equilibrium constants $K_{p_1}$ and $K_{p_2}$ for the reactions $A \rightleftharpoons 2 B$ and $P \rightleftharpoons Q + R$, respectively, are in the ratio of $2: 3$. If the degree of dissociation of $A$ and $P$ are equal, the ratio of the total pressure at equilibrium is,

• A. $1: 36$
• B. $1: 9$
• C. $1: 6$
• D. 1:4

Answer 1

Answer: (C)

At Equilibrium $1-\alpha \,\,\,\,2 \alpha$
Total moles $=1-\alpha+2 \alpha=1+\alpha$
$\therefore P_A=($ mole fraction of $A) \times$ Initial pressure $=$ $\left(\frac{1-\alpha}{1+\alpha}\right) P_1$
Similarly $P_B=\left(\frac{2 \alpha}{1+\alpha}\right) P$
$\therefore K_{p_1}=\frac{\left(P_B\right)^2}{\left(P_A\right)}=\frac{\left[\left(\frac{2 \alpha}{1+\alpha}\right) P_1\right]^2}{\left(\frac{1-\alpha}{1+\alpha}\right) P_1}=\frac{4 \alpha^2 P_1}{\left(1-\alpha^2\right)}$

$\therefore P_p=\left(\frac{1-\alpha}{1+\alpha}\right) P_2 ; P_Q=\left(\frac{\alpha}{1+\alpha}\right) P_2 ;$
$P_R=\left(\frac{\alpha}{1+\alpha}\right) P_2$
$K_{p_2}=\frac{P_R \times P_Q}{P_P}=\frac{\left(\frac{\alpha}{1+\alpha}\right) P_2 \times\left(\frac{\alpha}{1+\alpha}\right) P_2}{\left(\frac{1-\alpha}{1+\alpha}\right) P_2}$
$=\frac{\alpha^2 P_2}{\left(1-\alpha^2\right)}$
$\therefore \frac{K_{p_1}}{K_{p_2}}=\frac{2}{3}$ (given) $=\frac{4 \not{\alpha}^2 P_1}{\not{\left(1 / \alpha^2\right)}} \times\left(\frac{\not{1 / \alpha^2}}{\not{\alpha^2} P_2}\right)=\frac{4 P_1}{P_2}$
$\therefore \frac{P_1}{P_2}=\frac{1}{6}$