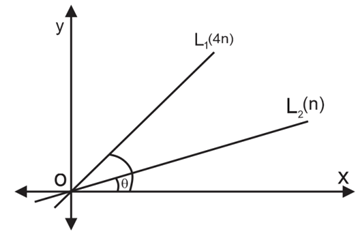
Question

The equations of the lines $L_{1}$ and $L_{2}$ are $y=mx$ and $y=nx,$ respectively. Suppose $L_{1}$ makes twice as large an angle with the horizontal (measured counterclockwise from the positive $x$ -axis) as does $L_{2}$ and $m=4n$ , then the value of $\frac{\left(m^{2} + 4 n^{2}\right)}{\left(m^{2} - 6 n^{2}\right)}$ is equal to (where, $n\neq 0$ )

• A. $3$
• B. $-3$
• C. $2$
• D. $-2$

Answer 1

Answer: (C)

Let, $m=tan 2 \theta $ and $n=tan \theta $
And $m=4n$ and $m\neq 0,$
$\therefore tan 2\theta \neq 0;\theta \neq 0$
$tan 2 \theta = 4 tan ⁡ \theta $
$\frac{2 tan \theta }{1 - tan^{2} ⁡ \theta }=4tan ⁡ \theta $
$\therefore 1=2-2tan^{2} \theta \Rightarrow 2tan^{2}⁡\theta =1$
$\Rightarrow tan^{2} \theta = \frac{1}{2}=n^{2}$
$\Rightarrow m^{2}=16n^{2}=8\Rightarrow \frac{m^{2} + 4 n^{2}}{m^{2} - 6 n^{2}}=\frac{10}{5}=2$