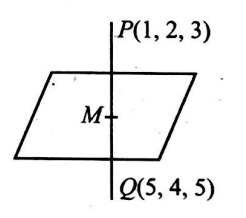
Question

The equation of the plane which has the property that the point $Q(5,4,5)$ is the reflection of point $P(1,2,3)$ through that plane, is $a x+ b y+ c z=d$ where $a, b, c, d \in N$. Find the least value of $(a+ b +c+ d)$.

Answer 1

Here midpoint is $M \equiv(3,3,4)$
and normal vector of the plane is parallel to $\overrightarrow{P Q}$
Hence $\vec{n}=4 \hat{i}+2 \hat{j}+2 \hat{k}=2(2 \hat{i}+\hat{j}+\hat{k})$

$\therefore $ Equation of plane passing through the midpoint $M$ of $P Q$, is
$2(x-3)+1(y-3)+1(z-4)=0$
$2 x +y+ z=13 \equiv a x +b y +c z=d$
$\Rightarrow a=2, b=1, c=1, d=13$
$\Rightarrow a+ b +c +d=17$