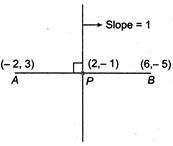
Q. The equation of the perpendicular bisector of the line segment joining $ A(-2,\text{ }3) $ and $ B(6,-5) $ is
Solution:
The equation of the line passing through the points $ (-2,3) $ and $ (6,-5) $ is $ (y-3)=\frac{-5-3}{6+2}(x+2) $
$ \Rightarrow $ $ (y-3)=-1(x+2) $
$ \Rightarrow $ $ y-3=-x-2 $
$ \Rightarrow $ $ y=-x+1 $ ..(i)
Now, the slope of perpendicular bisector of this line is
$=\frac{-1}{(-1)}=1 $ and the perpendicular bisector passing through the mid point of this line is $ (2,-1) $ . Then, equation of perpendicular bisector is $ (y+1)=1(x+2) $
$ \Rightarrow $ $ y+1=x-2 $
$ \Rightarrow $ $ x-y=3 $