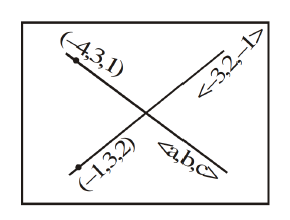
Q. The equation of the line passing through $(-4, 3, 1)$, parallel to the plane $x + 2y - z - 5 = 0$ and intersecting the line $\frac{x+1}{-3} = \frac{y-3}{2} =\frac{z-2}{-1} $ is :
Solution:
Normal vector of plane containing two intersecting lines is parallel to vector.
$\left(\vec{V}_{1}\right) = \begin{vmatrix}\hat{i}&\hat{j}&\hat{k}\\ 3&0&1\\ -3&2&-1\end{vmatrix}$
$ = -2 \hat{i} +6 \hat{k}$
$\therefore $ Required line is parallel to vector
$ \left(\vec{V}_{2}\right) = \begin{pmatrix}\hat{i}&\hat{j}&\hat{k}\\ 1&2&-1\\ -2&0&6\end{pmatrix} = 3\hat{i} - \hat{j} + \hat{k} $
$\Rightarrow $ Required equation of line is
$ \frac{x+4}{3} = \frac{y-3}{-1} = \frac{z-1}{1} $