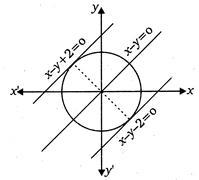
Question

The equation of the circle having $ x-y-2=0 $ and $ x-y+2=0 $ as two tangents and $ x-y=0 $ as a diameter is

• A. $ {{x}^{2}}+{{y}^{2}}+2x-2y+1=0 $
• B. $ {{x}^{2}}+{{y}^{2}}-2x+2y-1=0 $
• C. $ {{x}^{2}}+{{y}^{2}}=2 $
• D. $ {{x}^{2}}+{{y}^{2}}=1 $

Answer 1

Answer: (C)

Since, the equations of tangents $ x-y-2=0 $ and $ x-y+2=0 $ are parallel. $ \therefore $ Distance between them = diameter of the circle $ =\frac{2-(-2)}{\sqrt{{{1}^{2}}+{{1}^{2}}}} $ $ \left( \because \frac{{{C}_{2}}-{{C}_{1}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right) $ $ =\frac{4}{\sqrt{2}}=2\sqrt{2} $
$ \therefore $ Radius $ =\frac{1}{2}(2\sqrt{2})=\sqrt{2} $ It is clear from the figure that centre lies on the origin. $ \therefore $ Equation of circle is $ {{(x-0)}^{2}}+{{(y-0)}^{2}}={{(\sqrt{2})}^{2}} $ $ \Rightarrow $ $ {{x}^{2}}+{{y}^{2}}=2 $