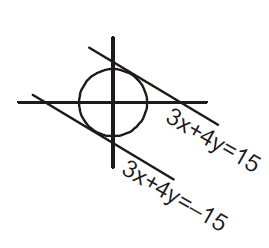
Question

The equation of a line parallel to the line $3x + 4y = 0$ and touching the circle $x^2 + y^2 = 9$ in the first quadrant is

• A. $3x + 4y = 15$
• B. $3x + 4y = 45$
• C. $3x + 4y = 9$
• D. $3x + 4y = 27$

Answer 1

Answer: (A)

Let, the equation be $3x + 4y = k$
then, $y=- \frac{3}{4}x+\frac{k}{4}$. By condition of tangency $\left(\frac{k}{4}\right)^{2}=9\left(1+\left(\frac{-3}{4}\right)^{2}\right) \Rightarrow k =\pm 15$
$3x + 4y = 15$ touches in the first quadrant.