Question

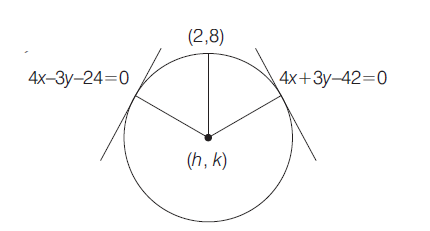
The equation of a circle passing through the point $(2,8)$, touching the lines
$4\, x-3 \,y-24=0$ and $4 \,x+3 \,y-42=0$ and
having the $x$ coordinate of its centre less than or equal to $8$ is

• A. $x^{2}+y^{2}+2 x-8 y-8=0$
• B. $x^{2}+y^{2}-4 x-6 y-12=0$
• C. $x^{2}+y^{2}+4 x-10 y+4=0$
• D. $x^{2}+y^{2}-6 x-4 y-24=0$

Answer 1

Answer: (B)

By the property of distance,
$\left|\frac{4 \,h-3 \,k-24}{5}\right|=\left|\frac{4 \,h+3,k-42}{5}\right|$
$=\sqrt{(h-2)^{2}+(k-8)^{2}}$
$\Rightarrow 4 \,h-3 \,k-24=\pm(4 \,h+3 \,k-42)$
either $4,h-3 k-24=4 h+3 k-42$
$\Rightarrow 6 \,k=18 \Rightarrow k=3$
or $\quad 4\, h-3 k-24=-4 h-3 k+42$
$\Rightarrow 8 \,h=66$
$\Rightarrow h=\frac{66}{8}=\frac{33}{4}>8$
Now, $(4h-3 k-24)^{2}=25\left[(h-2)^{2}+(k-8)^{2}\right]$
By solving this, we get, $h=2$
$\therefore $ Centre is $(2,3)$
Now, required circle is $(x-2)^{2}+(y-3)^{2}=25$
$\Rightarrow x^{2}+4-4 x+y^{2}+9-6 \,y=25$
$\Rightarrow x^{2}+y^{2}-4\, x-6 x=12$