Q.
The energy stored in the capacitor (in $μJ$ ) between terminals $a$ and $b$ of the network (as shown in figure) is $\frac{n}{2}μJ$ . Fin the value of $n$ . If capacitance of each capacitor is $1μF$ .
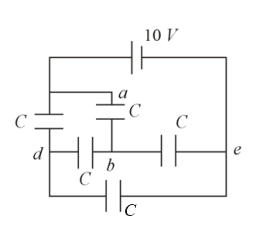
NTA AbhyasNTA Abhyas 2022
Solution:
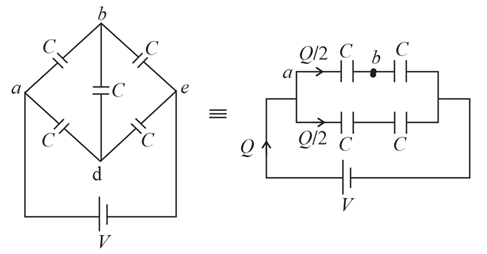
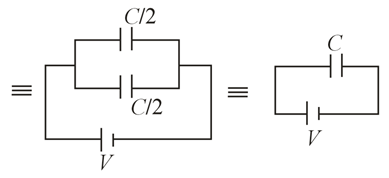 $\Rightarrow C_{e q}=C$
$\Rightarrow C_{e q}=C$