Question

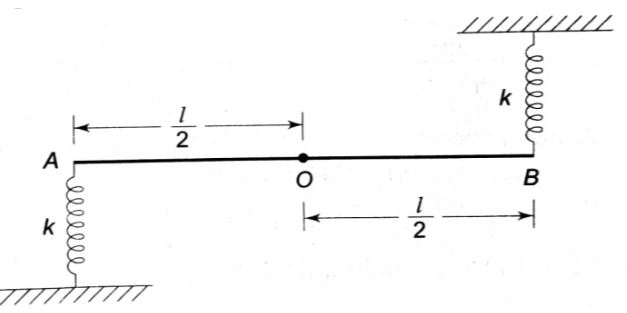
The ends of a rod of length $l$ and mass $m$ are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre $O$ . The rod is depressed slightly at end $A$ and released. The time period of the oscillation is

• A. $2\pi \sqrt{\frac{m}{2 k}}$
• B. $2\pi \sqrt{\frac{2 m}{k}}$
• C. $\pi \sqrt{\frac{2 m}{3 k}}$
• D. $\pi \sqrt{\frac{3 m}{2 k}}$

Answer 1

Answer: (C)

Let the rod be depressed by a small amount $x$ (in the figure). Both the springs are compressed by $x$ . When the rod is released, the restoring torque is given by
$\tau=\left(kx\right)\times \frac{1}{2}+\left(kx\right)\times \frac{1}{2}=\left(kx\right)1$
Now $tan\theta =\frac{x}{1 / 2}=\frac{2 x}{l}$ .
Since $\theta $ is small, $tan\theta \simeq \theta $ , where $\theta $ is expressed in radian.
Thus $\theta =\frac{2 x}{l}$ or $x=\frac{\theta l}{2}$
$\tau=k\left(\frac{\theta 1}{2}\right)\times 1=\frac{\left(k\theta 1\right)^{2}}{2}$

If $I$ is the moment of inertia of the rod about $O$ , then
$I\frac{d^{2} \theta }{\left(dt\right)^{2}}=-\left(\frac{\left(kl\right)^{2}}{2}\right)\theta $
Or $\frac{d^{2} \theta }{\left(dt\right)^{2}}=-\left(\frac{\left(kl\right)^{2}}{2 I}\right)\theta $
Since $\frac{d^{2} \theta }{\left(dt\right)^{2}} \propto \left(- \theta \right)$ , the motion is simple harmonic whose angular frequency is given by
$\omega =\sqrt{\frac{kl^{2}}{2 I}}$
Now, $\omega =\frac{2 \pi }{T}$ and $I=\frac{ml^{2}}{12}$ . Therefore, we have
$\frac{2 \pi }{T}=\sqrt{\frac{kl^{2}}{2} \times \frac{12}{ml^{2}}}=\sqrt{\frac{6 k}{m}}$
Or $T=\pi \sqrt{\frac{2 m}{3 k}}, \, $ which is choice $\pi \sqrt{\frac{2 m}{3 k}}$