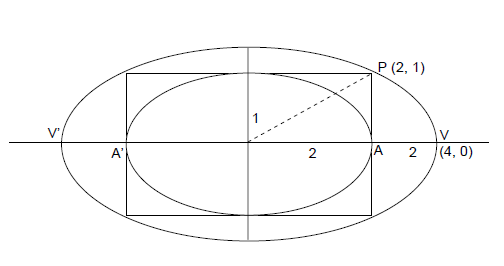
Q. The ellipse $x^2 + 4y^2 = 4$ is inscribed in a rectangle aligned with the coordinate axes, which in turn in inscribed in another ellipse that passes through the point $(4, 0)$. Then the equation of the ellipse is
AIEEEAIEEE 2009Conic Sections
Solution:
$x^{2}+4y^{2}=4 \Rightarrow \frac{x^{2}}{4}+\frac{y^{2}}{1}=1 \Rightarrow a=2, b=1 \Rightarrow P=\left(2, 1\right)$
Required Ellipse is $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \Rightarrow \frac{x^{2}}{4^{2}}+\frac{y^{2}}{b^{2}}=1$
$\left(2, 1\right)$ lies on it
$\Rightarrow \frac{4}{16}+\frac{1}{b^{2}}=1 \Rightarrow \frac{1}{b^{2}}=1-\frac{1}{4}=\frac{3}{4} \Rightarrow b^{2}=\frac{4}{3}$
$\therefore \frac{x^{2}}{16}+\frac{y^{2}}{\left(\frac{4}{3}\right)}=1 \Rightarrow \frac{x^{2}}{16}+\frac{3y^{2}}{4}=1 \Rightarrow x^{2}+12y^{2}=16$