Q.
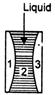
The effective focal length of the lens combination shown in the figure in - 60 cm. The radii of curvature of the curved surfaces of the Plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is: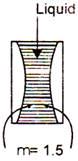
EAMCETEAMCET 2006Ray Optics and Optical Instruments
Solution:
The system is equivalent to combination of three lenses in contact, i.e.,
$ \frac{1}{F}=\frac{1}{{{f}_{1}}}+\frac{1}{{{f}_{2}}}+\frac{1}{{{f}_{3}}} $ But by lens Makers formula $ \frac{1}{{{f}_{1}}}=(1.5-1)\left( \frac{1}{-\infty }-\frac{1}{-12} \right)=0.5\times \frac{1}{12}=\frac{1}{24} $ $ \frac{1}{{{f}_{2}}}=(\mu -1)\left( \frac{1}{-12}-\frac{1}{12} \right)=-\left( \frac{\mu -1}{6} \right) $ $ \frac{1}{{{f}_{3}}}=(1.5-1)\left( \frac{1}{12}-\frac{1}{\infty } \right)=\frac{1}{24} $ Also $ F=-60\,cm $ $ \therefore $ $ \frac{1}{-60}=\frac{1}{24}-\frac{(\mu -1)}{6}+\frac{1}{24}=-\frac{(\mu -1)}{6}+\frac{1}{12} $ or $ \frac{(\mu -1)}{6}=\frac{1}{12}+\frac{1}{60} $ or $ \frac{(\mu -1)}{6}=\frac{5+1}{60}+\frac{6}{60} $ or $ (\mu -1)=\frac{36}{60}=0.6 $ or $ \mu =0.6+1=1.6 $