Q.
The $E^{\circ}$ in the given diagram is :-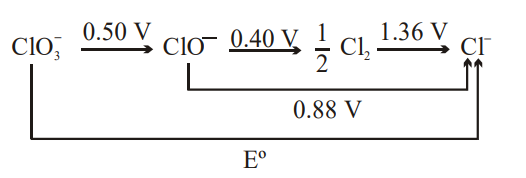
Electrochemistry
Solution:
$\underset{+5}{ClO_3^-} \to \underset{+1}{ClO^-}$
$n_1 = 4$
$E_1^{\circ} = 0.50$
$ \Delta G^{\circ}_1$
$\underset{+1}{ClO^-} \to \frac{1}{2} \underset{0}{Cl_2}$
$n_2 = 1$
$E_2^{\circ} = 0.40$
$ \Delta G^{\circ}_2$
$\frac{1}{2}\underset{0}{Cl_2} \to \underset{-1}{Cl^-}$
$n_3 = 1$
$E_3^{\circ} = 1.36$
$ \Delta G^{\circ}_3$
$\underset{+5}{ClO_3^-} \to \underset{-1}{Cl^-}$
$n = 6$
$E^{\circ} =0$
$ \Delta G^{\circ}_4 = $ ?
$\Delta G ^{\circ}=\Delta G _{1}^{0}+\Delta G _{2}^{0}+\Delta G _{3}^{0}$
$nE ^{\circ}= n _{1} E _{1}^{0}+ n _{2} E _{2}^{0}+ n _{3} E _{3}^{0}$
$E ^{o}=\frac{4 \times 0.50+1 \times 0.40+1 \times 1.36}{6}$
$ \Rightarrow 0.63 \,volt$
| $\underset{+5}{ClO_3^-} \to \underset{+1}{ClO^-}$ | $n_1 = 4$ | $E_1^{\circ} = 0.50$ | $ \Delta G^{\circ}_1$ |
| $\underset{+1}{ClO^-} \to \frac{1}{2} \underset{0}{Cl_2}$ | $n_2 = 1$ | $E_2^{\circ} = 0.40$ | $ \Delta G^{\circ}_2$ |
| $\frac{1}{2}\underset{0}{Cl_2} \to \underset{-1}{Cl^-}$ | $n_3 = 1$ | $E_3^{\circ} = 1.36$ | $ \Delta G^{\circ}_3$ |
| $\underset{+5}{ClO_3^-} \to \underset{-1}{Cl^-}$ | $n = 6$ | $E^{\circ} =0$ | $ \Delta G^{\circ}_4 = $ ? |