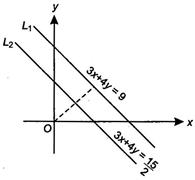
Q. The distance between the lines $ 3x+4y=9 $ and $ 6x+8y=15 $ is
Jharkhand CECEJharkhand CECE 2008
Solution:
If coefficient of $ x $ and $ y $ of both the lines are same, then the lines are parallel
Given, equation of lines are $ 3x+4y=9 $ ... (i) and $ 6x+8y=15 $
$ \Rightarrow $ $ 3x+4y=\frac{15}{2} $ ... (ii)
$ \therefore $ Both lines are parallel, therefore the distance between two lines $ =\frac{\left| \frac{15}{2}-9 \right|}{\sqrt{{{3}^{2}}+{{4}^{2}}}} $
$ =\frac{|15-18|}{2\sqrt{25}} $
$ =\frac{3}{2\cdot 5}=\frac{3}{10} $
Alternative The perpendicular distance from origin to the line
$ {{L}_{1}} $ is
$ {{d}_{1}}=\frac{9}{\sqrt{{{3}^{2}}+{{4}^{2}}}}=\frac{9}{5} $ and $ {{d}_{2}}=\frac{\frac{15}{2}}{\sqrt{{{3}^{2}}+{{4}^{2}}}} $
$ =\frac{15}{2\cdot 5}=\frac{15}{10} $
$ \therefore $ Distance between $ {{L}_{1}} $ and $ {{L}_{2}} $ is $ d={{d}_{1}}-{{d}_{2}} $ $ =\frac{9}{5}-\frac{15}{10}=\frac{18-15}{10} $
$ =\frac{3}{10} $