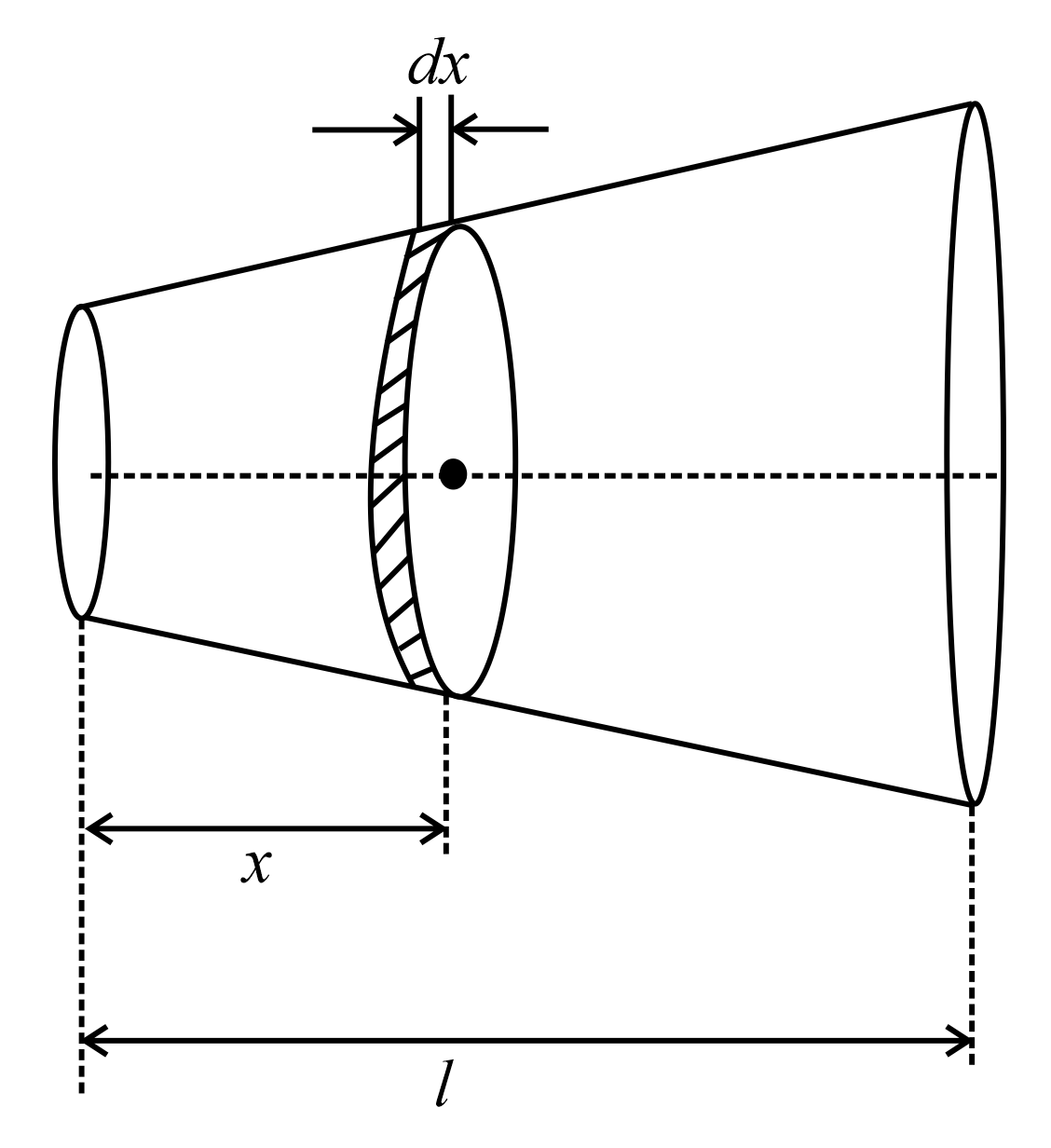
Question

The diameter of a rod is given by $d=d_{0}\left(\right.1+ax\left.\right)$ where $a$ is a constant and $x$ is the distance from one end. If the thermal conductivity of the material is $K,$ what is the thermal resistance of the rod if length is $l$ .

• A. $\frac{1}{ K \pi d_{0}^{2}}$
• B. $\frac{4 l}{K \pi d_{0}^{2} \left(\right. a l + 1 \left.\right)}$
• C. $\frac{2 l}{K \pi d_{0}^{2} \left(\right. a l + 1 \left.\right)^{2}}$
• D. $\frac{2 l}{K \pi d_{0}^{2} \left(\right. a l + 1 \left.\right)}$

Answer 1

Answer: (B)

Thermal resistance of a rod is given by,
$R_{th}=\frac{1}{K}\frac{l}{A}$
Where,
$K \rightarrow $ Thermal conductivity of the material of the rod,
$l \rightarrow $ Length of the rod and
$A \rightarrow $ Cross-sectional area of the rod.
Given,
Diameter of the rod at a distance $x$ from one end of the rod is,
$d=d_{0}\left(\right.1+ax\left.\right)$ .
That is, the thickness of the rod increases from one end to the other end.
Let's consider an elementary disc of thickness $dx$ at a distance $x$ from one end as shown below:

Thermal resistance of this elementary disc is given by,
$dR=\frac{1}{K}\frac{d x}{A}=\frac{1}{K}\frac{d x}{\pi \left(\frac{d}{2}\right)^{2}}$
$\Rightarrow dR=\frac{4}{K}\frac{d x}{\pi \left(d_{0}\left(\right.1+ax\left.\right)\right)^{2}}$
$\Rightarrow dR=\frac{4}{\pi d_{0}^{2} K}\frac{d x}{\left(1+ax\right)^{2}}$
The thermal resistance of the whole rod can be determined by,
$\int\limits _{0}^{R}dR=\frac{4}{\pi d_{0}^{2} K}\int\limits _{0}^{l}\frac{d x}{\left(1+ax\right)^{2}}$
$\Rightarrow R=\frac{4}{\pi d_{0}^{2} K}\frac{1}{a}\left[\frac{- 1}{1 + a x}\right]_{0}^{l}$
$\Rightarrow R=\frac{4}{\pi a d_{0}^{2} K}\left[\frac{- 1}{1 + a \left(l\right)} - \frac{- 1}{1 + a \left(0\right)}\right]$
$\Rightarrow R=\frac{4}{\pi a d_{0}^{2} K}\left[1 - \frac{1}{1 + a l}\right]$
$\Rightarrow R=\frac{4}{\pi a d_{0}^{2} K}\left[\frac{a l}{1 + a l}\right]$
$\Rightarrow R=\frac{4 l}{K \pi d_{0}^{2} \left(1 + a l\right)}$