Q.
The diagram shows the adiabatic curve for $n$ moles of an ideal gas. The bulk modulus for the gas corresponding to the point $P$ will be
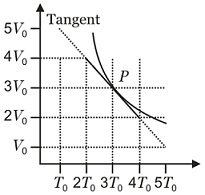
NTA AbhyasNTA Abhyas 2020Thermodynamics
Solution:

Solution: