Question

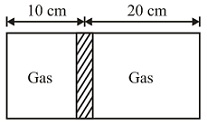
The diagram shows a horizontal cylindrical container of length $30 \, cm$ , which is partitioned by a tight-fitting separator. The separator is diathermic but conducts heat very slowly. Initially, the separator is in the state shown in the diagram. The temperature of the left part of the cylinder is $100 \, K$ and that on the right part is $400 \, K$ . Initially the separator is in equilibrium. As heat is conducted from the right to left part, separator displaces to the right. Find the displacement of separator (in $cm$ ) after a long when gases on the two parts of the cylinder are in thermal equilibrium.

Answer 1

It is given that initially, the separator is in equilibrium; thus pressure on both sides of the gas is equal say, it is P_i. If A be the area of cross-section of cylinder, number of moles of gas in the left and right part, n₁ and n₂, can be given as
$n_{1}=\frac{P_{\text{i}} \left(1 0 \text{A}\right)}{R \left(1 0 0\right)}$
and $n_{2}=\frac{P_{\text{i}} \left(2 0 \text{A}\right)}{R \left(4 0 0\right)}$
Finally, if the separator is displaced to right by a distance x,
we have
$n_{1}=\frac{\left(\textit{P}\right)_{f \text{i}} \left(1 0 + \textit{x}\right) \textit{A}}{\left(\textit{RT}\right)_{f ⁡}}$
and $\left(\textit{n}\right)_{2}=\frac{\left(\textit{P}\right)_{f } \left(2 0 - \textit{x}\right) \textit{A}}{\left(\textit{RT}\right)_{f ⁡}}$
Here $\text{P}_{f }$ and $\text{T}_{f }$ are the final pressure and temperature on both sides after a long time.
Now if we equate the ratio of moles n₁/n₂ in initial and final states, we get
$\frac{\left(\textit{n}\right)_{1}}{\left(\textit{n}\right)_{2}}=\frac{\left(1 0 \textit{A} / 1 0 0\right)}{\left(2 0 \textit{A} / 4 0 0\right)}=\frac{\left(1 0 + \textit{x}\right) \textit{A}}{\left(2 0 - \textit{x}\right) \textit{A}}$
$2\left(2 0 - \textit{x}\right)=10+\textit{x}$
$\textit{x}=10 \, cm$
Thus in the final state when gases in both parts are in thermal equilibrium, the piston is displaced 10 cm rightward from its initial position.